A Árvore Binária de Busca é uma estrutura de dados hierárquica e ordenada, projetada para armazenar, buscar e organizar informações de forma eficiente.
Ela é uma variação da árvore binária, com uma regra especial de ordenação que facilita a localização de elementos.
Propriedade Fundamental
Em uma árvore de busca binária, cada nó segue a seguinte regra:
- Todos os valores menores que o valor do nó atual estão à esquerda.
- Todos os valores maiores estão à direita.
Essa organização permite realizar buscas rápidas, de forma semelhante ao algoritmo de busca binária em listas ordenadas.
Percursos Clássicos (Traversals)
- Pré-Ordem (Pre-order) → Raiz → Esquerda → Direita
- Em-Ordem (In-order) → Esquerda → Raiz → Direita (gera valores ordenados)
- Pós-Ordem (Post-order) → Esquerda → Direita → Raiz
O percurso em-ordem é o mais utilizado para listar os elementos da BST em ordem crescente.
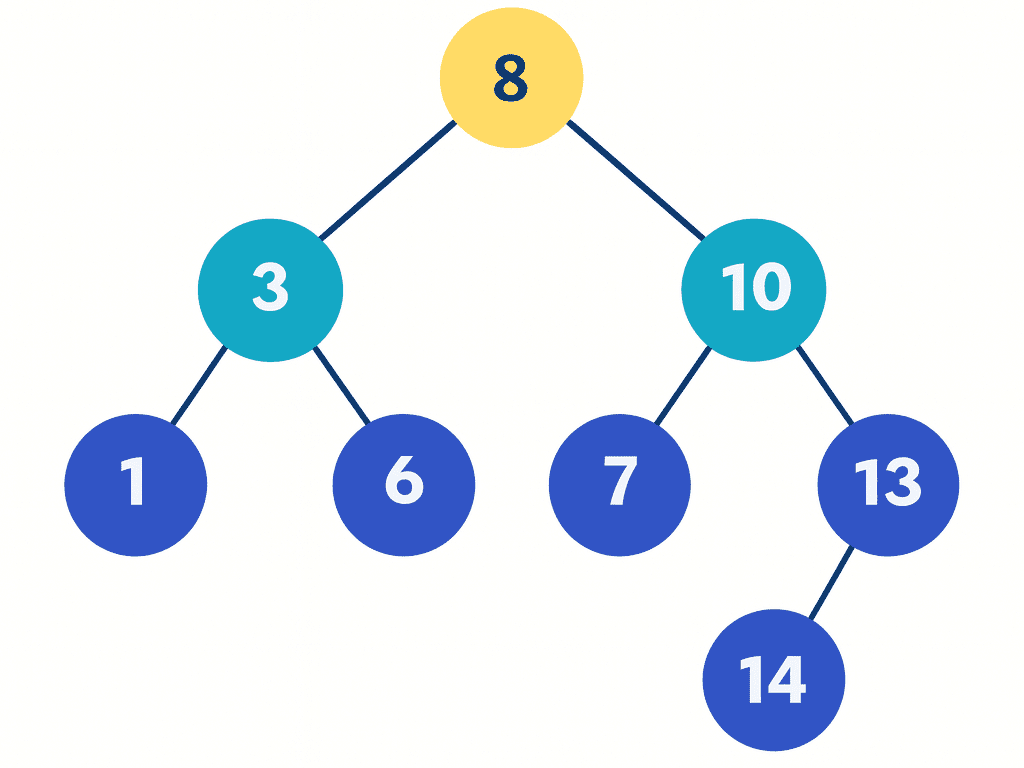
Percursos passo a passo (usando a árvore do desenho)
Árvore (valores): 8, 3, 10, 1, 6, 14, 4, 7, 13
🌿 1️⃣ Percurso Pré-Ordem (Pre-Order)
Ordem: Raiz → Esquerda → Direita
📘 Passo a passo:
- Visita o nó 8 (raiz)
- Vai para a subárvore esquerda (3)
- Desce para 1
- Volta e visita 6
- Retorna à raiz e vai para a direita (10)
- Visita 7, 13 e 14
✅ Resultado:
👉 8 → 3 → 1 → 6 → 10 → 7 → 13 → 14
🍃 2️⃣ Percurso Em-Ordem (In-Order)
Ordem: Esquerda → Raiz → Direita
📘 Passo a passo:
- Começa na subárvore esquerda de 8
- Visita 1, depois 3, depois 6
- Volta à raiz (8)
- Vai à direita e percorre 7, 10, 13 e 14
✅ Resultado:
👉 1 → 3 → 6 → 8 → 7 → 10 → 13 → 14
3) Pós-ordem (Esquerda → Direita → Raiz)
Visita o nó após os filhos.
- 1 → 4 → 7 → 6 → 3 → 13 → 14 → 10 → 8
Se quiser, faço mais 3 imagens no mesmo padrão (uma para cada percurso), mostrando a ordem de visita destacada com números.
Ordem: Esquerda → Direita → Raiz
📘 Passo a passo:
- Percorre toda a subárvore esquerda (1, 6, 3)
- Depois a subárvore direita (7, 14, 13, 10)
- Finaliza na raiz (8)
✅ Resultado:
👉 1 → 6 → 3 → 7 → 14 → 13 → 10 → 8